NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Khunti K, Griffin S, Brennan A, et al. Behavioural interventions to promote physical activity in a multiethnic population at high risk of diabetes: PROPELS three-arm RCT. Southampton (UK): NIHR Journals Library; 2021 Dec. (Health Technology Assessment, No. 25.77.)

Behavioural interventions to promote physical activity in a multiethnic population at high risk of diabetes: PROPELS three-arm RCT.
Show detailsTwo cost-effectiveness analyses were undertaken. The primary analysis was a model-based analysis using the School for Public Health Research Diabetes Prevention Model (henceforth ‘the model’).70 The secondary analysis was an alongside-trial analysis. The methods for the cost-effectiveness analyses are presented in the following order:
- calculating the costs of the interventions
- primary analysis – model-based evaluation
- secondary analysis – alongside-trial analysis.
Calculating the costs of the interventions
Intervention costs
Two sets of intervention costs were calculated: one relating to the estimated costs of delivering Walking Away and Walking Away Plus, given that it is likely to be delivered in real-world practice, and the second relating to the cost of delivering Walking Away and Walking Away Plus, as per the PROPELS trial protocol. The former set was developed in consultation with personnel involved in delivering Walking Away and related interventions, and was intended to represent the most likely costs faced by the NHS were Walking Away or Walking Away Plus to be implemented. The intention is to correct for any artificially high or low implementation costs that may be an artefact of the trial process. The real-world costs were used in the base-case analyses.
The Walking Away intervention costs included educator and administrative staff time, physical resources (e.g. pedometers and teaching materials), venue hire and refreshments, staff training and participant expenses. In addition, there were further costs that applied only to the Walking Away Plus arm, namely the cost of follow-up telephone calls and text messages.
The trial management group anticipated that, in a real-world setting, staff would need to be retrained less frequently than the 4 years of the trial would suggest. Therefore, the cost of training staff was annuitised over 10 years (in line with assumptions made for similar structured education interventions114) using the following annuity calculation:
where r = discount rate (3.5%) and n = expected lifetime of the training (10 years).
In the trial, participants from both intervention arms attended the same education sessions; therefore, the common costs were totalled and divided proportionally to the number of participants randomised to each arm. The Walking Away Plus additional costs were added to this to yield a total cost per arm that was divided by the number randomised to produce a per-participant cost for each arm.
Economic analysis methods
Two analyses were undertaken: a model-based evaluation (primary analysis) and a within-trial analysis (secondary analysis). Details of both of these analyses are given below. This section details aspects of the analyses that were in common across both analyses.
Perspective, discounting and time horizon
In line with the NICE methods guide,75 the analyses took an NHS and a Personal Social Services perspective; future costs and QALYs were discounted at a rate of 3.5% per annum; and the time horizon was a lifetime horizon in the primary analysis and a 4-year time horizon in the secondary analysis.
Outcome measures
Costs and QALYs were estimated for each strategy.
The primary outcome measure was the ICER, which is change in cost/change in QALYs. As there are three strategies in this decision problem, the strategies were ordered by the total number of QALYs produced and ICERs were calculated comparing each strategy to the next least effective strategy. Any intervention that was dominated (i.e. produced fewer QALYs at a higher cost than another intervention) or was extendedly dominated (i.e. if a strategy’s ICER is higher than the ICER of the next most effective intervention) then these strategies were removed when calculating ICERs.
The value of information was calculated for this decision problem. We calculated the value of expected value of perfect information (EVPI). This statistic is the value to a decision-maker (e.g. NICE) of eliminating the uncertainty in all parameters in the economic analysis. Therefore, it provides an upper limit on any future research to reduce uncertainty on these sets of strategies. We also calculated the parameter EVPI, which is the value to the decision-maker of eliminating all uncertainty in a subset of parameters in the model, for step count, diabetes diagnoses and HbA1c.
Primary analysis: model-based evaluation
A detailed account of the methodology underlying the model is reported elsewhere.70 In brief, it was an individual patient-level simulation in which simulated individuals were passed through a lifetime of events in annual cycles. During each annual cycle, an individual may be diagnosed with diabetes, may become unwell (from cardiovascular disease, cancer, diabetes-related complications, depression, dementia or osteoarthritis), may be prescribed antihypertensives, statins or diabetes medication, or may die (either from their illness or from background mortality). Their risk of each of these events happening is determined by a series of risk functions and the individual’s metabolic characteristics. These metabolic characteristics were set at the start of the model and updated with each annual cycle based on observations in the PROPELS trial and on modelled trajectories.115 Each time an individual experiences a clinical event, passes into a new health state or is prescribed a new medication, this is associated with costs and health consequences. Thus, the model can extrapolate intervention effects and estimate costs and QALYs over a lifetime horizon. The model takes an NHS and Personal Social Services perspective.
The model is well validated for use in diabetes prevention interventions,73,116 but further development was required to adapt it specifically to the PROPELS trial. In particular, the following adaptations were made:
- The model used a simulated population based on the Health Survey for England. This was changed to better represent the PROPELS trial population.
- Step count was included as a new population characteristic. This directly affected the cardiovascular risk of modelled individuals based on the results of the NAVIGATOR trial.20
- During the first four annual model cycles, the pre-existing HbA1c trajectories and diabetes diagnosis mechanism were replaced by a new regression models developed using the trial data, so that diabetes diagnoses reflected those observed in the trial.
The model population
To model the cost-effectiveness of Walking Away and Walking Away Plus in the general population, we ran the model twice for each analysis: once with a population representing the South Asian trial subpopulation, and once with a population representing the non-South Asian trial subpopulation. The results from the two subgroups were weighted using data from the UK government117 on the relative size of these two populations in the UK. For example, if we found that a strategy resulted in 10 discounted QALYs being accrued in the non-south Asian population and 11 discounted QALYs being accrued in the South Asian population, and if 10% of the population was South Asian, then the total number of discounted QALYs accrued for that strategy would be 10.1, because (11 × 0.1) + (10 × 0.9) = 10.1.
Each of these subpopulations was synthesised based on an analysis of the trial participants at baseline, using the following steps:
- assessment of the distribution of each continuous variable required by the model (e.g. height, weight and systolic blood pressure)
- transformation of any non-normally distributed variables to generate approximately normal distributions for each variable
- construction of a multivariate normal distribution using all variables (both continuous and categorical) simultaneously to preserve correlations between variables
- sampling of each variable for all simulated individuals
- for continuous variables:
- – generation of cut-off points for each categorical variable using the proportional frequency of each category in the PROPELS data
- – the sampled variable was converted back into the appropriate category using these cut-off points.
- back-transformation of any transformed variables to the natural scale.
Step count modelling
At baseline, step count was sampled from a multivariate normal distribution as described previously. At 12 and 48 months, step count was simulated using a beta-regression. Beta-regressions predict two outcomes: a mean effect and dispersion in the mean effect. Variance can be predicted for any mean effect and dispersion using the following formula:
Furthermore, beta-regressions require that the data that are being predicted are on a scale between 0 and 1. We transformed step count so that 0 was equivalent to 1 step lower than the lowest value in the PROPELS trial (464 steps per day) and 1 was equivalent to 1 step per day more than the highest value in the PROPELS trial (25,341 steps per day).
The key advantage of this approach is that it allows heterogeneity to be included in the simulation because we know the expected number of steps per day and the expected variance in the number of steps per day for every individual. This means that we do not have to assume that an average treatment effect is appropriate, with the level of heterogeneity in identical individual outcomes being driven by the data.
In line with the statistical analysis, to estimate step count at 4 years we controlled for two indicator variables for randomised study arm (Walking Away vs. control, Walking Away Plus vs. control), the three randomisation stratification variables (centre, ethnicity and sex), ambulatory activity at baseline and ambulatory activity at 1 year as covariates. Unlike in the statistical analysis, we did not include wear time at baseline, wear time at 48 months, number of valid days at baseline or number of valid days at 48 months as covariates in the regression model, as predicting these covariates in our simulation model would have increased the computational complexity of the simulation and the causal linkages between these parameters and measured step count were unclear. We applied these control variables to both the mean effect and the dispersion parameters of the beta regression, with the exception of ethnicity for the dispersion parameter, as the models failed to converge when this covariate was included.
To estimate step count at 1 year, we controlled for two indicator variables for randomised study arm (Walking Away vs. control, and Walking Away Plus vs. control), the three randomisation stratification variables (centre, ethnicity and sex) and ambulatory activity at baseline as covariates. We applied these control variables to both the mean effect and the dispersion parameters of the beta-regression, again with the exception of ethnicity for the dispersion parameter.
As the beta-regression produces data on the mean and variance for each individual in the model, we simulated each individual’s step count by randomly sampling this from their individualised beta-distribution (based on their expected mean step count and expected dispersion). We did this separately for each individual’s step count at 1 and 4 years. After we had sampled each individual’s step counts (on the 0–1 scale), we transformed these simulated values back into steps per day. Between 0–12 and 12–48 months, step count was assumed to be linear. Beyond 48 months, step count was extrapolated based on four different possible scenarios. First, an underlying trajectory for step count was estimated by constructing an ordinary least squares linear regression model of step count and age at baseline, adjusted for sex, site, intervention arm and ethnicity from the PROPELS data. The coefficient for age from this model was used as the underlying annual change in step count in a no-intervention scenario for each individual. The observed step count was then compared with this underlying trajectory in the following four scenarios (Figure 6):
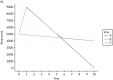
FIGURE 6
Example step count trajectories. In each scenario, line A represents the individual’s trajectory between years 1 and 4, line B represents the underlying trajectory, and line C represents the modelled step count.
- A. Step count increased between 0 and 12 months and then declined to 48 months, but was above the underlying trajectory at 48 months. In this case, step count would continue to decline at the same rate as between 12 and 48 months until it converged with the underlying trajectory, at which point the individual switched to the underlying trajectory.
- B. The inverse case of (A) – step count decreased between 0 and 12 months and then increased to 48 months but remained below the underlying trajectory. In this case, the step count would continue to increase at the same rate as between 12 and 48 months until it converged with the underlying trajectory.
- C. An individual experienced improvement during the trial such that their 48-month step count was above the underlying trajectory and step count had increased between 12 and 48 months. In such a case, the individual would not converge with the underlying trajectory were their rate of change to continue. In such a case, the annual rate of change for the underlying trajectory would be applied after 48 months such that the individual step count trajectory was parallel to the underlying trajectory.
- D. The inverse case of (C) – the individual experienced a decline in step count from 12 to 48 months and their 48-month step count was below the underlying trajectory. In this case, the annual rate of change for the underlying trajectory was applied after 48 months such that the individual’s trajectory was parallel to the underlying trajectory.
Step count and QRISK
It was assumed that the unadjusted QRISK2 algorithms currently in the model adequately described the baseline risk of cardiovascular disease (CVD) for an individual with the average baseline step count in the PROPELS trial.
A QRISK2 modifier was calculated for each individual in the model, based on model 3 (the fully adjusted model) from the NAVIGATOR analysis.20 This analysis was a Cox’s proportional hazards model, which concluded that the hazard of cardiovascular events was reduced by 10% for every 2000-step increment at baseline and that a change from baseline of 2000 steps in 12 months was independently associated with an 8% reduction in cardiovascular event rate.
From this, per-step hazard changes were calculated by finding the 2000th root of 0.9 and 0.92, respectively. Individual hazard ratios for each patient were calculated, which adjusted for their baseline ambulatory activity and the change in step count that they experienced in the RCT. These hazard ratios were recalculated every year. The formulae for calculating each individual’s hazard ratio is as follows:
Therefore, each individual had a hazard ratio at baseline depending on their baseline ambulatory activity, which was updated every 12 months depending on their change in ambulatory activity. The individual-estimated rate of having a CVD event within the next year (as currently calculated in the existing model structure using the QRISK2 algorithm) was multiplied by the annual hazard ratio to adjust the risk of CVD events according to individual step count.
HbA1c trajectories
As for step count, we used beta-regressions to estimate HbA1c levels at 1 and 4 years due to their advantages in being able to incorporate heterogeneity. HbA1c was transformed so that 4.5% (0.1% lower than the smallest value in the PROPELS trial) was equal to 0%, and 9.2% (0.1% higher than the largest value in the PROPELS trial) was equal to 1.
To estimate HbA1c levels at 4 years, we controlled for two indicator variables for randomised study arm (Walking Away vs. control, and Walking Away Plus vs. control), HbA1c at 1 year, the three randomisation stratification variables (centre, ethnicity and sex) and HbA1c at baseline as covariates. We applied these control variables to both the mean effect and the dispersion parameters of the beta regression.
To estimate HbA1c at 1 year we controlled for two indicator variables for randomised study arm (Walking Away vs. control, and Walking Away Plus vs. control), the three randomisation stratification variables (centre, ethnicity and sex) and HbA1c at baseline as covariates. We applied these control variables to both the mean effect and the dispersion parameters of the beta regression.
Between 1 and 4 years we assumed that HbA1c levels changed linearly between the two time points. After 4 years, we assumed that HbA1c in the treatment was maintained or declined in the same way that we have assumed that step count was maintained or declined (see Step count modelling). From the fifth year onwards, the HbA1c levels of individuals are estimated using the Breeze et al.115 trajectory models.
Modelling uncertainty
To assess uncertainty in the model, we ran both deterministic analyses and PSAs. In the deterministic case, we set all model parameters to their mean values. The model ran one fixed simulated population. In the PSA, we varied all model parameters simultaneously within their distributions and performed many different model runs. We used this set of PSA results to estimate mean costs and QALYs, and also calculated 95% CIs around these point estimates. Initially, we ran 1000 different sets of parameters. We assessed the results for stability using Hatswell et al.’s118 criteria, and performed more PSA runs when needed.
We further explored the sources of model uncertainty using value-of-information analysis, which estimated the potential cost to the decision-maker of making the wrong decision owing to uncertainty around the results. We used Sheffield Accelerated Value of Information71 to do this. We assumed that the maximum number of people affected by the decision was equivalent to the number of people expected to be offered the National Diabetes Prevention Programme (a similar intervention that is currently being rolled out nationally), namely 100,000 per year,119 and that the decision would be relevant for 10 years.
Threshold analysis
We conducted a threshold analysis to determine the justifiable cost of the interventions for them to be cost-effective relative to usual care at a maximum acceptable ICER of £20,000 per QALY. To do this, we used a rearranged incremental net monetary benefit equation:
Secondary analysis: alongside-trial analysis
The alongside-trial analysis incorporated all of the costs incurred and health benefits accrued during the 4-year trial period. All statistical analysis was conducted in R version 3.5.3.120
Costs
The costs that each participant incurred included the cost of the intervention (methods described previously), the cost of health-care resource use and the cost of medications taken during the trial period. Data on resource use were collected in the trial and data on unit costs were obtained from nationally representative sources. Within the trial, participants were asked about resource usage within the past 12 months at 0, 12 and 48 months. Resource use in years 2 and 3 was assumed to be the same as at 48 months. Costs incurred in years 2, 3 and 4 were discounted at 3.5% per year.20
Resource use
Self-reported data on health-care resource use at baseline and at 12 and 48 months were taken from the PROPELS data, namely the number of times in the last 12 months that they had used each of the following health-care resources: GP, practice nurse, other health-care professional, attendance at accident and emergency, outpatient clinics, day hospital and inpatient stays. Costs of these resources were obtained from the PSSRU121 and NHS reference costs122 and are summarised in Table 12.
TABLE 12
Resource use and medication costs
Medications
Self-reported data on medication use at baseline and at 12 and 48 months were taken from the PROPELS data. It was assumed that a participant who was taking one or more of these medications was doing so long term and was expected to be taking the medication for the duration of the trial. If a participant was found to have been taking a medication at 48 months, but not at 12 months, the date of their commencing medication was assumed to be midway between these time points (i.e. 30 months). The cost of 1 year of treatment on each medication type was taken from the Regional Drug and Therapeutics Centre (Newcastle) Cost Comparison Charts.79 It was assumed that participants had been prescribed the most commonly prescribed preparation of each medication class (as reported in the Prescription Costs Analysis120). The annual cost of treatment with the drugs included is shown in Table 12.
Utilities
The benefits of the intervention arms were estimated QALYs, calculated from EuroQol-5 Dimensions, five-level version (EQ-5D-5L), scores.123 In line with current NICE recommendations, utility values were generated by mapping the EQ-5D-5L domain scores to EQ-5D-3L value set. Individual 5L dimension scores were mapped to 3L scores using the van Hout algorithm.122 The mapped 3L scores were aggregated into health state indices, which were valued using the Dolan et al.79 valuation model.
Quality-adjusted life-years
Per-participant QALYs were calculated from the utility values using the area-under-the-curve method. In line with the NICE methods guide,20 QALYs for years 2, 3 and 4 were discounted at 3.5% per year.
Cost–utility analysis
The incremental costs and benefits of the interventions were calculated using seemingly unrelated regression equations, implemented using the systemfit package in R.119 The equation system comprised two equations:
The fitted covariates included site, age, sex, ethnicity, and baseline costs and QALYs.
Results are presented as incremental costs, incremental QALYs, ICERs and incremental net monetary benefit, assuming a willingness-to-pay threshold of £20,000 per QALY in line with NICE guidelines.75
Scenario analyses and multiple imputation
In addition to the two sets of intervention costs described above, the analyses were performed using both complete cases and imputed data. For the latter, data were imputed using the mice (multiple imputation by chained equations) function in R.124 Five imputed data sets were generated using the predictive mean matching option. The imputation models included all of the covariates used in the systemfit models. As it was not possible to run systemfit models directly using imputation models, the systemfit models were run separately for each imputed data set and the results were pooled manually using Rubin’s rules.124
Results
Trial intervention costs
For reasons of practicality, participants in both the Walking Away and the Walking Away Plus arms attended the same structured education sessions. Therefore, in costing the interventions, it was assumed that the costs incurred in providing each arm were the same, except for the telephone and text message support costs, which were assigned only to the Walking Away Plus arm. The full details and unit costs used in the microcosting of the interventions are provided in Appendix 11, Tables 49 and 50.
Educators
The cost of providing an educator for 1 hour was £20.37 (including on-costs). The sessions lasted 4 hours, giving a per-session cost of £81.48. A total of 259 sessions were delivered by two educators and 123 sessions were delivered by one educator.
Delivery of the interventions was supported by a training and mentoring package, which comprised:
- Training to deliver –
- the initial Walking Away structured education sessions (both intervention arms)
- the Walking Away update sessions (both intervention arms)
- the follow-up telephone calls (Walking Away Plus only).
- Mentoring to promote the fidelity of –
- the Walking Away sessions (both intervention arms)
- the telephone calls (Walking Away Plus only).
Training was delivered by two members of NHS staff: one at band 7 and one at band 8a. Fidelity promotion was carried out by the band 8a staff member only. For clarity, ‘trainers’ refers to the staff members who delivered the training sessions and ‘educators’ refers to the individuals who attended the training sessions and delivered the structured education sessions in the interventions.
Walking Away delivery training
All educators (eight in Leicester and four in Cambridge) attended the Walking Away training. One session was run in each site. Nine educators (five in Leicester and four in Cambridge) attended the update training sessions. One update training session was run in each site. Details of the total costs of running these training sessions are provided in Table 13.
TABLE 13
The total cost of all training sessions and fidelity assessments delivered in the trial
Telephone call delivery training
Initially, all educators were trained to deliver the telephone calls. Throughout the study, there was a high staff turnover for this part of the intervention, as educators were unwilling to make the telephone calls, and replacement staff were trained to take over. The total telephone call training costs were £4071, details of which are given in Table 13.
Walking Away fidelity training
There were two types of sessions to promote fidelity of the Walking Away education sessions: in year 1, educators were observed delivering the intervention; in years 2–4, they met with trainers for mentorship and support. The total Walking Away fidelity training cost was £3393, details of which are given in Table 14. Fidelity assessment of the telephone calls was conducted separately, and this cost £1803, details of which are provided in Table 13.
TABLE 14
Total training costs (£)
Total intervention costs
The annual cost is the total cost divided by the annuity factor. Four-year costs are the annual costs of training multiplied by 4. The total training costs for both interventions are given in Table 14.
Support staff costs
Two types of support staff, administrators and project managers were employed to assist organisation of the interventions. The trial management team estimated that it took each administrator 15 minutes to book an appointment for a participant, and 30 minutes per education session to book the venue, prepare resources and process invoices. Administrators at Cambridge were paid university grade 2 salaries and at Leicester the staff were at NHS band 3; project managers were at university grade 6 at Cambridge and NHS band 6 at Leicester. For Cambridge staff, the mean salary (including on-costs) for each grade was used to estimate annual salary. Hourly rates for grade 2 staff were calculated based on a 35-hour working week. In the case of Leicester staff, the mean salary for a band 6 hospital-based professional staff member including overheads was taken from the Personal Social Services Research Unit (PSSRU). Equivalent figures for band 3 were not available, so the hourly rate for a band 3 staff member was estimated using the ratio of hourly pay to hourly total cost for a band 4 staff member. The costs of employing these staff are shown in Table 15.
TABLE 15
Cost of support staff
Text message system
The total number of text messages sent in the trial was 96,252. Each text cost 3.5 pence to send. In addition, there was an annual licence fee of £118 for the system, giving a total cost of text messages of £3841.
Participant expenses
Participant travel expenses were reimbursed on request at both sites. Leicester did not reimburse mileage but did pay for participants’ taxis, whereas Cambridge did reimburse mileage but did not pay for taxis. The total cost of travel expenses across the two sites was £6454.19.
Administration consumables and teaching resources
Participants in both Cambridge and Leicester were sent appointment letters by post. The Leicester site also sent participants a map showing where to go for the appointment. Costs were associated with teaching resources (paper, pens and booklets) and sets of demonstration materials. In total, the cost of administration and consumables came to £11,163.
Venue costs
In addition to the cost of staff to deliver the sessions, costs were incurred for venue hire and providing refreshments. Some venues provided refreshments in house, whereas at other sessions the refreshments were provided by the PROPELS team. The total cost of booking venues came to £9924.
Additional costs
In addition, each participant received a pedometer that cost £10.50.
Real-world cost assumptions
Following communication with personnel involved in delivering Walking Away and related interventions in a real-world setting (specifically the DESMOND National Director, Bernie Stribling, who is familiar with the intervention landscape for all Walking Away sites in the UK and Ireland), a second set of costs was estimated to reflect the expected cost of delivering the interventions outside the trial. The differences between the two sets of costs are summarised in Table 16. It is assumed that, in the real-world setting, either Walking Away or Walking Away Plus would be commissioned.
TABLE 16
Real-world vs. PROPELS assumptions
Per-participant costs
The per-participant costs are summarised in Table 17. The total within-trial cost of delivering Walking Away was £286 per participant and the cost of delivering Walking Away Plus was £338 per participant. The real-world costs of delivering the interventions are estimated to be slightly lower than the within-trial costs (Walking Away £257, Walking Away Plus £322). There are two primary reasons for the real-world costs being so close to the within-trial costs of delivering Walking Away. First, the staff members who would be expected to deliver the interventions in the real world are more expensive than the staff used in the PROPELS RCT. Second, we expect that fewer sessions per year will be delivered in real-world settings, increasing the effective per-participant cost of training the educators.
TABLE 17
Within-trial and real-world per-person costs (£)
Alongside-trial analysis
Within-trial costs
Health-care resource use
Per-participant health-care resource use at baseline was slightly higher in the Walking Away (£620) and Walking Away Plus arms (£626) than in the usual care arm (£717). A detailed breakdown of the costs incurred during the trial is provided in Appendix 13, Table 69. In summary, health-care resource use was higher in the Walking Away arm than in the usual care arm, and higher still in the Walking Away Plus arm. Although primary care costs were similar across the arms, the Walking Away and Walking Away Plus arms both incurred higher hospital inpatient and outpatient costs.
Adjusted costs and quality-adjusted life-years
Table 18 shows the costs results of the systemfit models over our four scenarios, which cover imputation techniques and methods for calculating the costs of Walking Away and Walking Away Plus. estimating the difference between arms. In all scenarios, both the Walking Away and the Walking Away Plus arms incurred more total costs over the study period than the usual care arm.
TABLE 18
Adjusted costs and QALYs from the seemingly unrelated regressions
Table 18 shows the QALY results of the systemfit models estimating the difference between arms. In all scenarios, both Walking Away and Walking Away Plus accrued more QALYs over the study period than the usual care arm, with the Walking Away arm accruing more QALYs than usual care. However, the incremental QALYs between either intervention and usual care are much lower than that observed in the complete-case analysis. It is unsurprising that the results may be substantially different between the imputed and the complete cases, as only 678 patients in the PROPELS data had complete cost and QALY data.
Cost-effectiveness
The ICERs from the within-trial analysis for the real-world costs and complete-case data are given in Table 19. When one QALY is valued at £20,000, in line with NICE guidelines, the within-trial analysis would indicate that Walking Away is the most cost-effective option. These results are highly volatile and are sensitive to the assumptions made about missing data and the calculation of the costs. For example, when trial costs are used and the missing data are imputed, usual care would be the most cost-effective option when one QALY is valued at £20,000. It should be noted that all within-trial results are highly uncertain.
TABLE 19
Within-trial cost-effectiveness when real-world costs and complete-case data are used
This uncertainty is illustrated on the cost-effectiveness plane in Figure 7. Interventions on the cost-effectiveness plane to the right of the dotted line are cost-effective at a willingness-to-pay threshold of £20,000, and those to the left are not. As the 95% CIs for cost and QALYs for both interventions cross the dotted line, it is not possible to be certain if either intervention is cost-effective at this threshold.
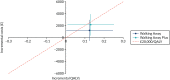
FIGURE 7
Cost-effectiveness plane showing within-trial adjusted incremental costs and QALYs.
Similarly, the cost-effectiveness acceptability curve in Figure 8 demonstrates this uncertainty. The graph shows the probability that each of the three trial arms is cost-effective at varying values of a QALY. At a low willingness-to-pay threshold, usual care has the highest chance of being the most cost-effective intervention because it is the cheapest option. As the value of a QALY increases, the QALY gains in Walking Away and Walking Away Plus become more valuable and their relative chance of cost-effectiveness increases. Between the upper and lower limits of the NICE threshold, namely £20,000 and £30,000 per QALY, the three arms have a roughly even chance of being the most cost-effective option.
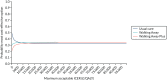
FIGURE 8
Cost-effectiveness acceptability curve showing within-trial data.
Model results
Model population
The characteristics of the simulated population compared with the real PROPELS data at baseline are shown in Appendix 10, Table 48. Overall, there was good agreement between the simulated and the real data.
Step count trajectories
The figures below show the step count trajectories in the South Asian (Figure 9) and non-South Asian (Figure 10) populations in the deterministic model runs. The average per-day step count at baseline in the non-South Asian population was 7164 (in all three arms). At 12 months, both Walking Away and Walking Away Plus arms were given increases in step count to reflect the treatment effect of the interventions, resulting in average daily step counts of 7342 and 7563, respectively. By 48 months, the average daily step count had declined to 6981 and 7174, respectively.

FIGURE 9
Step count trajectories in the South Asian population.
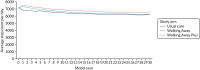
FIGURE 10
Step count trajectories in the non-South Asian population.
In the Asian population, the baseline step count was 7042 steps per day. At 12 months, it rose to 7178 and 7399 steps per day in the Walking Away and Walking Away Plus arms, respectively. Over the next 3 years, to the end of the trial period at 48 months, step count declined in both groups, to 7075 and 7301 steps per day, respectively.
Beyond 4 years in both subpopulations, both Walking Away and Walking Away Plus individuals converged with their individual underlying trajectory, and then continued to decline in daily step count at a rate of 67 steps per day per year, as predicted by the ordinary least squares regression model. At an aggregate level, there is some noise to this effect as individuals die, and those with a low step count (and higher cardiovascular risk) are at higher risk of mortality. Note that average step count beyond 30 years is omitted from these graphs as the small numbers of individuals make the figures unstable.
HbA1c and diabetes diagnoses
Table 20 shows the rates of diagnosis of T2D in the deterministic model runs in the non-South Asian and South Asian populations. In both subpopulations, the total number of within-trial diagnoses was largest in the Walking Away arm, followed by the usual care arm, followed by the Walking Away Plus arm. This was expected because our logistic regressions (see Appendix 12, Tables 51–68) produced odds ratios for rates of diabetes diagnosis comparing Walking Away with usual care of 1.55 (97.5% CI 0.52 to 4.63) at year 1 and 1.58 (97.5% CI 0.74 to 3.39) at year 4. Comparing Walking Away Plus with usual care, the odds ratios for the rates of diabetes diagnoses were 0.72 (97.5% CI 0.19 to 2.68) at year 1 and 1.25 (97.5% CI 0.57 to 2.74) at year 4. In all three arms, rates of diabetes diagnosis over a lifetime were higher in the South Asian population than the in the non-South Asian population.
TABLE 20
Diabetes diagnoses in the South Asian and non-South Asian populations
As shown in Figures 11 and 12, the average HbA1c level (%) was very similar across all three trial arms. The trajectory for the first 4 years (i.e. the data generated from analysis of the PROPELS trial) was not notably different from that for the subsequent years of the model (which was extrapolated using equations based on an analysis of the Whitehall data set125).
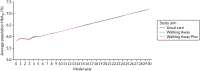
FIGURE 11
The HbA1c trajectory in the South Asian population.
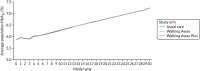
FIGURE 12
The HbA1c trajectory in the non-South Asian population.
Deterministic results
In the deterministic analysis, mean parameter values were used and the population was fixed. The costs and QALYs for each subpopulation and the weighted population are given in Table 21. All results are presented per person. In both the South Asian and the non-South Asian subpopulations, Walking Away is both more expensive and less effective than usual care, that is it is dominated. In both subpopulations, Walking Away Plus is more expensive and slightly more effective than usual care, giving ICERs that are well in excess of the £20,000-per-QALY threshold.
TABLE 21
Deterministic cost-effectiveness results in all three analysis populations
Probabilistic sensitivity analysis
The PSA results for each subpopulation are given in Table 22. In both the South Asian and the non-South Asian subpopulations, Walking Away is both more expensive and less effective than usual care, that is it is dominated by usual care. In both subpopulations, Walking Away Plus is more expensive and slightly more effective than usual care, giving ICERs that are well in excess of the £20,000-per-QALY threshold.
TABLE 22
Probabilistic sensitivity analysis results (South Asian, non-South Asian and weighted populations)
The cost-effectiveness planes (Figures 13–15) for both subpopulations and the weighted population show that the PSA mean ICERs for both Walking Away (dark blue crosses) and Walking Away Plus (light-blue crosses) are to the left of the dotted line that indicates a cost-effectiveness threshold of £20,000 per QALY; that is, they are not cost-effective at this threshold. However, the purple and light-blue clouds of points that indicate individual PSA runs show that, for some combinations of parameters, the results are to the right of the line, indicating that both or either of the interventions could be cost-effective at this threshold.
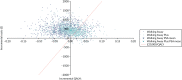
FIGURE 13
Cost-effectiveness plane for the model results in the South Asian population.
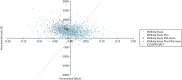
FIGURE 15
Cost-effectiveness plane for the model results in the weighted population.
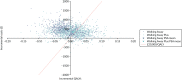
FIGURE 14
Cost-effectiveness plane for the model results in the non-South Asian population.
As shown by the cost-effectiveness acceptability curve in Figure 16, among the non-South Asian population, at a threshold of £20,000 per QALY there is a 52.0% chance that usual care is the most cost-effective option, a 9.8% chance that Walking Away is the most-cost-effective option and a 38.2% chance that Walking Away Plus is the most cost-effective option. At a threshold of £30,000 per QALY, the corresponding probabilities are 45.5%, 11.9% and 42.5%.
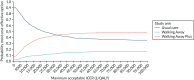
FIGURE 16
Cost-effectiveness acceptability curve (non-South Asian population).
Among the Asian population (Figure 17), at a threshold of £20,000 per QALY there is a 61.8% chance that usual care is the most cost-effective option, an 11.7% chance that Walking Away is the most cost-effective option and a 26.4% chance that Walking Away Plus is the most cost-effective option. At a threshold of £30,000 per QALY, the corresponding probabilities are 54.6%, 14.0% and 31.4%, respectively.
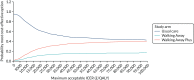
FIGURE 17
Cost-effectiveness acceptability curve (South Asian population).
Among the weighted population (Figure 18), there is a 55.6% chance that usual care is the most cost-effective option at £20,000 per QALY, a 9.5% chance that Walking Away is the most cost-effective and a 34.9% chance that Walking Away Plus is the most cost-effective. At a threshold of £30,000 per QALY, the corresponding probabilities are 48.6%, 11.4% and 40.0%, respectively.
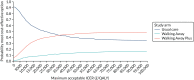
FIGURE 18
Cost-effectiveness acceptability curve (weighted population).
Clinical events
Table 23 shows the PSA average lifetime per-person incidence of T2D, CVD and T2D complications in each of the two subpopulations.
TABLE 23
Clinical events in the PSA: South Asian and non-South Asian populations
Intervention cost threshold analyses
Table 24 shows the results of the intervention cost threshold analysis. Walking Away Plus would need to be delivered at a cost of £116 per person to be cost-effective at a threshold of £20,000 per QALY. Because Walking Away is less effective than usual care, it would have to be less expensive than usual care by £370 to be cost-effective at £20,000 per QALY.
TABLE 24
Intervention cost threshold analysis
Value of information
The total per-person EVPI was found to be £279.56. Assuming that the maximum number of interventions that would be delivered per year was 100,000, and that the decision relevance horizon was 10 years, the total EVPI for the UK is £279,559,484. This can be interpreted as the total value to the UK of research to eliminate all uncertainty about the cost-effectiveness of Walking Away and Walking Away Plus.
The expected value of perfect parameter information (EVPPI) for the key groups of parameters taken from the PROPELS trial are presented in Table 25 and Figure 19. The sources of uncertainty that have the largest potential impact on the decision are the parameters required to predict HbA1c and T2D diagnoses.
TABLE 25
The EVPPI for parameters from PROPELS trial
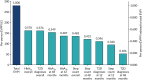
FIGURE 19
The EVPPI of parameters gathered from PROPELS data.
- Cost-effectiveness analysis - Behavioural interventions to promote physical acti...Cost-effectiveness analysis - Behavioural interventions to promote physical activity in a multiethnic population at high risk of diabetes: PROPELS three-arm RCT
- stmn2.L stathmin 2 L homeolog [Xenopus laevis]stmn2.L stathmin 2 L homeolog [Xenopus laevis]Gene ID:494676Gene
- znf367.S zinc finger protein 367 S homeolog [Xenopus laevis]znf367.S zinc finger protein 367 S homeolog [Xenopus laevis]Gene ID:443788Gene
Your browsing activity is empty.
Activity recording is turned off.
See more...