Mechanism of Action Assays for Enzymes

John Strelow; Walthere Dewe; Phillip W Iversen; Harold B Brooks; Jeffrey A Radding; James McGee; Jeffrey Weidner

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

Markossian S, Grossman A, Arkin M, et al., editors. Assay Guidance Manual [Internet]. Bethesda (MD): Eli Lilly & Company and the National Center for Advancing Translational Sciences; 2004-.

Mechanism of Action Assays for Enzymes^*

Authors

John Strelow, Walthere Dewe, Phillip W Iversen,¹ Harold B Brooks, Jeffrey A Radding, James McGee,² and Jeffrey Weidner³.

Affiliations

¹ Eli Lilly and Company

² Eli Lilly and Company

³ AbbVie, Chicago, IL

Published May 1, 2012; Last Update: October 1, 2012.

Abstract

Many drugs are inhibitors of enzymes involved in mediating the disease processes. Understanding the mechanism of action (MOA) of the target enzyme is critical in early discovery and development of drug candidates through extensive Structure-Activity Relationship (SAR) studies. This chapter contains a primer on the MOA of enzymes and its significance in drug discovery, types of inhibition, development and validation of MOA assays, data analysis and guidelines for performing these assays. New and experienced investigators will find this chapter useful when starting new projects involving enzyme targets.

Overview of MOA in Drug Discovery

The purpose of a mechanism of action (MOA) study is to characterize the interaction of a compound with its target to understand how the compound interacts with the target and how natural substrates at physiologic concentrations will modulate this activity. These compounds are often inhibitors of enzymes but only rarely become drugs due to the requirements for a drug to not only inhibit the target but to have acceptable solubility, permeability, protein binding, and selectivity, metabolism and toxicity profiles. This potential for the compound to become a drug is slowly revealed through the analysis and tracking of these characteristics, as chemistry elaborates the structure-activity relationship (SAR). As described in the body of this document, certain types of biochemical behavior are associated with good drug-like properties both in vitro and in vivo.

Most biochemical screens are designed to provide a chemical starting point based upon the most robust, simple and inexpensive modality for screening. This is due to the required reproducibility in the screening process and the potentially large number of molecules to be run through the screen. Most enzymatic screens are designed to identify inhibitors regardless of their mode of action. Thus, screens are usually run at or below the K_m for the substrate(s). In the case of an enzyme with two substrates, the screen is often designed to run under pseudo-first order kinetics by running the assay under conditions where one substrate is at saturation, well above its K_m, and the second is at or below its K_m for the enzyme. One can therefore identify inhibitors that have competitive, noncompetitive and uncompetitive behavior with regard to the substrate at or below K_m and noncompetitive or uncompetitive behavior with regard to the other substrate at well above its K_m for the enzyme.

In the drug discovery process, the screening phase casts a wide net and the ability to further analyze compounds in more detail is limited, therefore the number of actives isolated from a screen for follow-up are determined by the overall hit rate, the repeat rate upon retesting and determination of the IC₅₀ in a concentration response curve (CRC) test. In general, activities range from mid-micromolar to sub-micromolar for enzyme inhibitors right out of the screen. It is this piece of information (the IC₅₀), along with an analysis of the structural classes of active molecules by a medicinal chemist, which defines the initial SAR, if there is one in the data. It is after this initial analysis that MOA studies can prove valuable by further defining the nature of the inhibitor from a biochemical point of view. MOA studies at this point in the drug discovery process define the nature of the SAR by elucidating the type of inhibition by which the discovered molecules operate. Thus, one can define if the discovered inhibitor is competitive with substrate, for example, and as described below, potentially suffers from certain liabilities associated with this mechanism.

Cell based assays of biochemical actives are usually utilized to identify promising molecules in a second round of low to medium throughput screening. If a molecule shows significant activity in a cell based assay, then it continues through the flow scheme. The lack of cell based activity of biochemically potent actives is usually attributed to lack of cellular permeability, with a wave of the hand; however, an understanding the MOA of a compound at this stage can add depth to the interpretation of cellular activity or its absence. Knowing a compound is competitive with a substrate helps establish the binding pocket and, in combination with structural and SAR information, provides an immediate direction for further chemical synthesis. However, these competitive compounds with promising structure and potent biochemical activity might compete with a cellular substrate present at high intracellular concentration thus show no significant cell based activity. Alternatively, more potent cell based activity than is biochemically predicted from IC₅₀ curves might correlate with unusual kinetic behaviors such as slow binding behavior and/or slow off rates (tight binding). As there is no single, unique answer, biochemical MOA studies help in interpretation of cell based activities and provides further support for molecules with desirable characteristics to move forward in the flow scheme. Traditionally, as MOA studies were slow, laborious efforts, only a few selected molecules could be readily analyzed. With the advent of laboratory automation and enhanced data processing, it is now possible to assess a larger number of compounds rapidly. Therefore, it is feasible (and desirable) to examine the results of a screening campaign, in addition to standard cell based assays in the second tier, by an analysis of MOA.

Types of Inhibition

There are three main types of inhibition (competitive, noncompetitive, and uncompetitive) that are most commonly used to describe the binding of an inhibitor to a target enzyme (Figure 1). However, a complete analysis of the mechanism of action requires the scientist to also evaluate other potential inhibition events, including allosteric, partial, tight-binding, and time-dependent inhibition. A review of these types of inhibition is provided in the sections that follow.

Competitive Inhibition

A competitive inhibitor binds only to free enzyme. Often this binding event occurs on the active site of the target, precisely where substrate also binds. Although this is the case for a majority of competitive inhibitors, it is a misleading oversimplification. It is more appropriate to state that the binding of a competitive inhibitor and the binding of substrate are mutually exclusive events. Figure 2 provides illustrations of some possible mutually exclusive binding events.

Despite the differences in binding to the free enzyme illustrated in Figure 2, all competitive inhibitors have the same effects on substrate binding and catalysis. A competitive inhibitor will raise the apparent K_m value for its substrate with no change in the apparent V_max value. As a result, it is often stated that competitive inhibition can be overcome, observed by an increase in the apparent K_i value, at higher concentrations of substrate. This characteristic will have physiological consequences on the observed efficacy of drugs. As an enzyme’s reaction is inhibited by a competitive inhibitor, there is an increase in the local concentration of substrate. Without a mechanism to clear the substrate, a competitive inhibitor will lose potency. This is not the case for a noncompetitive inhibitor.

Noncompetitive Inhibition

A noncompetitive inhibitor binds equally well to both free enzyme and the enzyme-substrate complex. These binding events occur exclusively at a site distinct from the precise active site occupied by substrate. Figure 3 provides some illustrations of the more common noncompetitive binding events.

In contrast to a competitive inhibitor, a noncompetitive inhibitor will lower the apparent V_max value, yet there is no effect on the apparent K_m value for its substrate. Essentially, the K_i of the inhibitor does not change as a function of the substrate concentration.

In some circumstances, a compound may have unequal affinity for both free enzyme and the enzyme-substrate complex. This mixture of competitive and noncompetitive phenotypes is called mixed inhibition.

Uncompetitive Inhibition

An uncompetitive inhibitor binds exclusively to the enzyme-substrate complex yielding an inactive enzyme-substrate-inhibitor complex (Figure 4). When encountered, the apparent V_max value and the apparent K_m value should both decrease. Despite their rarity in drug discovery programs, uncompetitive inhibitors could have dramatic physiological consequences. As the inhibitor decreases the enzyme activity, there is an increase in the local concentration of substrate. Without a mechanism to clear the buildup of substrate, the potency of the uncompetitive inhibitor will increase.

Allosteric Inhibition

An allosteric inhibitor decreases activity by binding to an allosteric site other than or in addition to the active site on the target. This interaction is characterized by a conformational change in the target enzyme that is required for inhibition. These conformational changes can affect the formation of the usual enzyme-substrate active site complex, stabilization of the transition state, or reduce the ability to lower the activation energy of catalysis. Figure 2e and Figure 3a are classical examples of allosteric inhibition. As such, an allosteric inhibitor may display a competitive, noncompetitive, or uncompetitive phenotype with respect to substrate binding.

Partial Inhibition

Partial inhibition results from the formation of an enzyme-substrate-inhibitor complex that can generate product with less facility than the enzyme-substrate complex. This can be illustrated in Figure 3a. When “I” is a partial inhibitor bound in the enzyme-substrate-inhibitor complex, the catalytic center may retain some ability to align near the substrate and facilitate catalysis. As a consequence of these structural changes, partial inhibitors can also be allosteric inhibitors of enzyme activity. In direct contrast, full inhibition results in an enzyme-substrate-inhibitor complex where the catalytic center is not capable of aligning near the substrate for catalysis.

Tight-Binding Inhibition

In this type of inhibition, the population of free, soluble inhibitor is significantly depleted by the formation of the enzyme-inhibitor or enzyme-substrate-inhibitor complex. While tight-binding inhibitors can bind to the target enzyme in a competitive, noncompetitive, or uncompetitive manner with respect to substrate binding, they can display noncompetitive phenotypes. However, a tight-binding inhibitor typically binds with an apparent affinity (K_i) near the concentration of enzyme (active sites) present in the biochemical assay.

Time-Dependent Inhibition

Time-dependent inhibitors bind slowly to the enzyme on the time scale of enzymatic turnover, thus displaying a change in initial velocity with time. This has the effect of slowing the observed onset of inhibition. Time-dependent inhibitors also impede the observed recovery of enzyme activity following inhibition, resulting in slow k_off values. As illustrated in Figure 5, these inhibitors typically yield nonlinear initial velocities and nonlinear recoveries of enzyme activity.

Interestingly, many successful therapeutic drugs are time-dependent inhibitors. For these inhibitors with slow k_off values, the rate of release of inhibitor from the enzyme-inhibitor complex (recovery of enzyme activity) proceeds independent of the substrate concentration and the physiological mechanism to remove inhibitor. This makes time-dependent inhibition a very attractive and proven strategy for the discovery and development of drugs.

Some time-dependent inhibitors covalently attach to the target enzyme. For those inhibitors, the k_off value is zero and the inhibition is said to be irreversible. These are typically less attractive molecules, unless the formation of the covalent species is specific to the reaction mechanism of the enzyme. Some inhibitors are for all practical purposes irreversible, with very low k_off values, despite their inability to covalently attach to the enzyme. This stands in direct contrast to rapid equilibrium, reversible inhibitors that bind to and release from the enzyme at rates that are rapid in comparison to the rate of enzyme turnover.

Performing MOA Studies

When performing classical steady-state mechanism of action studies, the scientist should carefully consider and incorporate the proper biochemical and statistical guidelines provided in this section. These guidelines should assist in the initial characterization of the enzyme-inhibitor complex. However, in some cases the classical steady-state experiment is not sufficient and additional characterizations are required. Examples include compounds that display tight-binding inhibition, time-dependent inhibition, covalent modification, or nonspecific inhibition of the enzyme. Therefore, we also provide guidelines to identify these additional types of inhibitors and plan the appropriate follow-up analysis.

Classical Steady-State Experiments

These types of studies involve measurements of the V_max and K_M of a substrate at a range of inhibitor concentrations. The scientist should refer to Basic Enzyme Assays chapter of this manual, for a description of how to perform measurements of the V_max and K_m for a substrate. As mentioned previously, changes in the apparent V_max and K_m give the scientist a view of the binding modality (competitive, noncompetitive, or uncompetitive) and the potency (K_i and K_i’). Figure 6 illustrates the classical steady-state experiment used to determine the binding modality and potency.

The methodology proposed here to determine the binding potency and modality of an inhibitor is derived from a steady-state model of enzyme kinetics. The term steady-state refers to a constant concentration of the enzyme-substrate complex present during the reaction. As summarized by Copeland (1) and Segal (2), there are several assumptions that simplify the mathematical treatment of the kinetics. When these assumptions fail, the steady-state MOA model proposed here is not valid.

1.: The enzyme is acting catalytically and the concentration of substrate is much greater than the concentration of enzyme.
2.: During the initial phase of the reaction (initial velocity), there is no buildup of any intermediate other than the enzyme-substrate complex.
3.: There is very little product formed over the course of the reaction so that the depletion of substrate is minimal and the reverse reaction is insignificant.
4.: The concentration of inhibitor is much greater than the concentration of enzyme so that the depletion of free inhibitor resulting from the formation of the enzyme-inhibitor complex is minimal.

The scientist should utilize the following guidelines in the design, execution, and analysis of a classical MOA experiment.

Guidelines for Assay Design

It is essential to ensure that the enzyme, substrate, co-factors, and buffer conditions have been fully evaluated and characterized. Wherever possible, the scientist should strive to achieve in vitro conditions that will best represent the physiological conditions in a robust, reproducible manner. The selection of these factors can have a large impact on the binding modality and potency observed.
An enzyme titration should be performed to determine the concentration of active sites in the assay. Consult Copeland, Enzyme 2ed, pg313 or an experienced enzymologist for more information (1).
There should be at least 5 concentrations of substrate tested, spanning a range of at least ½×K_m to 5×K_m, for each concentration of inhibitor tested. As illustrated in Figure 7, the ability to distinguish a competitive inhibitor from a noncompetitive or uncompetitive inhibitor is increasingly enhanced at concentrations of substrate above its K_m value. The ability to distinguish noncompetitive inhibition from uncompetitive inhibition is more challenging and can be improved with very accurate determinations of the apparent K_m. Therefore, the scientist should strive to judiciously increase the range and number of concentrations of substrate tested.
The plot of the [substrate] vs initial velocity should not display sigmoidal kinetics, unless it is a mechanistic feature of substrate binding and catalysis for that enzyme. The impact of sigmoidal kinetics on the K_m curve is illustrated in Figure 8. Sigmoidal kinetics may be a sign of an impure enzyme or the presence of multiple isoforms of the enzyme (ex. multiple phosphorylation states of the same kinase). Refer to Copeland, Enzyme 2ed, pg382 or an enzymologist experienced with sigmoidal kinetics (1).
The initial velocity should be measured. In order for the steady-state assumptions to hold, it is recommended that less than 10% of the substrate be converted to product. The chapter on Basic Enzyme Assays describes this in more detail. However, initial velocity conditions do not infer linearity and the user should refer to the guideline directly below.
The formation of product should be linear with respect to time. This is best achieved by measuring the rate of product formation at the chosen concentrations of substrate using the assay conditions, detection system, and instruments that will be used for the final assay. Linearity should be assessed visually from plots of the raw data.
There should be at least 8 concentrations of inhibitor tested at each concentration of substrate. The range of inhibitor concentrations tested should span the K_i or K_i’, depending on the binding modality. Reporting of binding constants outside of the range of concentrations tested should be avoided. It is also recommended to include inhibitor concentrations at or above ~10×K_i to ensure maximum inhibition and the identification of any potential partial inhibitors. It should be noted that any observation of partial inhibition could instead be a consequence of a compound’s poor solubility.
Where available, a control inhibitor should be evaluated under the exact conditions that will be used for the final assay.
In addition to the experimental wells containing a matrix of substrate and inhibitor dilutions, the final assay should include both high and low controls. The high control should contain the substrate titration without inhibitor to reflect the maximum enzyme activity at each substrate concentration. The low control should contain the substrate titration without enzyme or substrate and without inhibitor. The low controls should reflect the signal expected for no enzyme activity at each substrate concentration. Depending on the composition of the inhibitor stocks, DMSO might be needed in the control wells to assure consistency across all the experiments.
The concentration of DMSO should be kept constant in MOA experiments for a particular target. DMSO can have a significant impact on enzyme activity and the concentration of DMSO in the wells containing compound should be identical to the concentration of DMSO in the control wells (described directly above). DMSO can also impact the solubility of a compound and its observed potency. Therefore, the concentration of DMSO should be consistent in replicate MOA experiments (or in comparison to IC₅₀ experiments).
It is recommended to evaluate, in the standard assay conditions, dependence of [enzyme] on the IC₅₀ of the compounds to be tested. Shifts in the IC₅₀ as a function of the [enzyme] is an indication of tight-binding inhibition and/or solubility issues. When this is encountered, the scientist should consult with an enzymologist experienced with tight-binding inhibition.
If detergents are required for enzyme activity or automation, the scientist should strive to maintain their concentrations well below the critical micelle concentration (CMC). The formation of micelles, at high concentrations of detergents, can interfere with the determinations of the binding modality and potency. An exception to this rule would include assays requiring detergents as part of the mechanistic evaluation. If the assay can only be run above the CMC, the scientist should consult with an enzymologist experienced with lipids, micelles, and surface dilution kinetics.
The reaction should be measured under steady-state conditions that includes the following: 1) there should not be any appreciable buildup of any enzyme intermediates other than the ES complex, 2) the [substrate] should be >> [enzyme], and 3) the initial phase of the reaction is measured so that the [product] ~ 0, the depletion of substrate is minimal, and the reverse reaction is insignificant (1).
The concentration of a required cofactor should be >> [enzyme].

Statistical Validation of the Designed Assay

The requirements for statistical validation of a MOA assay can be divided into two situations: 1) high-throughput assays using automation that can test many compounds, and 2) low-throughput assays in which only one or a few compounds are tested. In the first case, a replicate-experiment study should be performed as described in the Assay Validation chapter of this manual. Briefly, 20 to 30 compounds should be tested in two independent runs. Then the MSD or MSR and limits of agreement are determined for each of the key results, including V_max, K_m, K_i, K_i’, and α or α_inv. Specific acceptance criteria have not been determined. The reproducibility should be judged as suitable or not for each situation. For low-throughput assays, a replicate-experiment study is not required. At a minimum, key results from the MOA experiment, such as V_max, K_m, and K_i, should be compared to previous/preliminary experiments to ensure consistency. The data from the MOA experiment should be examined graphically for outliers, goodness of fit of the model to the data, and consistency with the assumptions and guidelines for designing and running the assay (see Guidelines for Assay Design above and Guidelines for Running the Assay below).

Guidelines for Running the Assay

The assay should be run under the exact same conditions as developed using the guidelines above. In addition, the assay should be run within the timeframe where the reagents are known to be stable.
When a control inhibitor is included, then the K_i (and/or K_i’) value should be compared with legacy data to ensure robust, quality results. It is also recommended to include additional inhibitors with alternative binding modalities, if available.
The K_m and V_max values from the high controls and the signal from the low controls should be compared with the legacy values determined in identical conditions, as described above.
A standard curve should be included for detection systems yielding signals that are nonlinear with respect to the amount of product formed. This nonlinearity is a common feature in fluorescent-based assays. The standard curve should be used to covert the signal produced to the amount of product formed. The resulting amount of product formed over the course of the assay time should be used in the data fitting methodologies. Please refer to the Immunoassay Methods chapter.

Guidelines for Data Fitting and Interpretation

The multivariate dataset (v, [I],[S]) should be fit using a non-linear regression analysis with the appropriate models described below. Linear transformations of the data should be avoided as they will distort the error of the experiment and were historically used only before the introduction of computer algorithms.
The scientist should perform any necessary background corrections, before the multivariate fitting, so that a signal or rate of 0 represents that expected for conditions lacking enzyme activity. Depending on the assay design, this may include a single background correction applied to the entire experiment or several different corrections. The latter should be used when the background signal varies with the [substrate] tested. Here there should be a background correction for each [substrate] tested.

The traditional model of general mixed inhibition is:

Image enzymemoa-Image001.jpg

Where v is the speed of the reaction (slope of product formed vs. time), V_max is the upper asymptote, [S] is the substrate concentration, and [I] is the inhibitor concentration. See the glossary for definitions of K_m, K_i, and K_i’. This model can also be written as:

Image enzymemoa-Image002.jpg

Image enzymemoa-Image003.jpg

where α = 1/α_inv = K_i’/K_i. This model reduces to specific models for competitive, non-competitive, and un-competitive inhibition as described in Table 1.

Another form of this model that has better statistical properties, in terms of parameter estimation and error determination, is:

Image enzymemoa-Image004.jpg

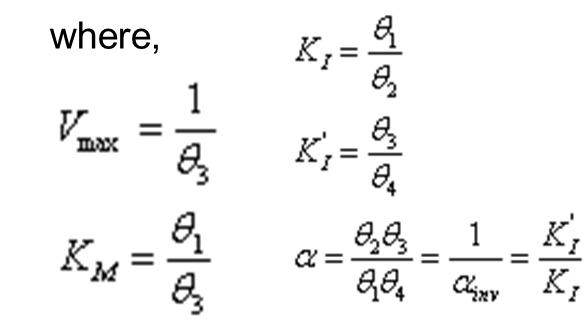
Image enzymemoa-Image005.jpg

More details on these models can be found in a manuscript in preparation by the primary authors of this chapter.

1.

Fit a robust multiple linear regression of 1/v vs. 1/[S], [I]/[S], and [I]. This provides starting values of the θ parameters for the non-linear regression in the next step.

2.

Fit model P4 to the data (v, [I], [S]).

3.

Calculate the parameters of interest from the θ values.

4.

Calculate confidence limits for each key parameter value using Monte Carlo simulation.

5.

Make decisions of mechanism based on the value of α or α_inv and the associated confidence limits.

α or α_inv should be used to assign the binding modality. If α is less than 1, the mechanism is:
a.
Uncompetitive if the upper confidence limit of α < 0.25
b.
Noncompetitive if the lower confidence limit of α > 0.25
c.
Not competitive, otherwise
If α_inv < 1, then the mechanism is:
a.
Competitive if the upper confidence limit of α < 0.1
b.
Noncompetitive if the lower confidence limit of α > 0.1
c.
Mixed, if both confident limits are within [0.1, 0.5]
d.
Not declarable, otherwise

The details of how these cutoffs were chosen are in a manuscript in preparation.

When the signal measured at 10×K_i (representing full enzyme inhibition by the compound) is >>0 (baseline corrected), the compound is displaying partial (and/or allosteric) Inhibition. This difference might also be observed when the incorrect conditions were chosen for the low control to represent no enzyme activity, if there was not enough inhibitor (relative to the K_i or K_i’) to achieve maximum inhibition, and/or if the compound tested is poorly soluble.
When the K_i or K_i’ resulting from the fit is within 10-fold of the concentration of active sites in the assay, the compound will start to display tight-binding inhibition. Inaccuracies in the binding modality and potency will result. In some cases where the inhibitor is not soluble, tight binding inhibition may exist at much higher K_i or K_i’ values. As recommended previously, the dependency of the enzyme concentration on the inhibitor’s potency is the best method to identify tight-binding inhibition. The scientist should consult with an expert in tight-binding inhibition to further characterize the inhibitor.
Data suggesting that a compound is noncompetitive (and in some cases mixed) should be handled with caution. Compounds that are time-dependent, irreversible, poorly soluble, nonspecific, and/or tight-binding will display a noncompetitive/mixed phenotype in this type of classical steady-state experiment. As such, it is critical to evaluate these additional potential mechanisms of action, described herein.
Additional recommendations for data analysis can be found in the next section.

When the Steady-State Assumptions Fail

The steady-state MOA model proposed for here for data fitting requires several important assumptions hold true. While a majority of these assumptions are covered in the previous sections, the invalidation of a few key assumptions should prompt the scientist to perform additional mechanistic characterizations. These key assumptions, a mechanism to flag their breakdown in the steady-state MOA model, and a recommended plan of action are presented.

Tight Binding Inhibition

The [inhibitor] in solution should be much greater than the [enzyme] in the assay. This assumption fails most frequently in 2 circumstances. First, some compounds bind to their target with such high affinity (_appK_i values within 10 fold of the [enzyme]) that the population of free inhibitor molecules is significantly depleted by formation of the EI complex. Second, some compounds are both very potent and poorly soluble. The poor solubility of the inhibitor will increase the observed _appK_i value (relative to the [enzyme]). In both cases, the compounds are called tight binding inhibitors.

How can tight binding inhibitors be flagged in the steady-state MOA model?
- Regardless of their true binding modality, they display a noncompetitive phenotype.
- They have observed _appK_i values between ½ and 10-fold of the [enzyme] in the assay.
- Poorly soluble compounds may also display tight binding inhibition. This is often masked by an inflated observed _appK_i value.
What is the recommended plan for an appropriate characterization?
- Calculate the dependence of the IC₅₀ values on the [enzyme]. Using a fixed concentration of substrate at K_m, the IC₅₀ of the inhibitor should be measured at ≥5 concentrations of enzyme. If the IC₅₀ changes significantly as a function of the [enzyme], the inhibitor is displaying tight binding properties and requires further characterization. If the IC₅₀ does not change significantly, the compound is not tight binding, this key assumption ([Inhibitor]>>[Enzyme]) is true, and the steady-state MOA model is valid. These two phenotypes are illustrated in Figure 9.
- Calculate the dependence of the IC₅₀ values on the [substrate]. Using a fixed concentration of enzyme, the IC₅₀ of the inhibitor should be measured at >5 concentrations of substrate. The range of concentrations of substrate should span the K_m (as recommended previously). As illustrated in Figure 10, the change in the IC₅₀ vs [substrate] is described by the equation listed below and yields the true binding potency (K_i and K_i’). The ratio of K_i’/K_i (termed alpha, α) reflects the binding modality. Inhibitors with alpha values statistically equal to 1.0 are noncompetitive, values statistically less than 1.0 are uncompetitive, and values statistically greater than 1.0 are competitive.

Model to Determine Tight Binding MOA:
Image enzymemoa-Image008.jpg

These methodologies are described in more detail in Chapter 9 of Enzymes 2^nded by Copeland (1). We also recommend consulting with a statistician and an enzymologist experienced with tight binding inhibition.

Time-Dependent Inhibition

When the reaction is started with enzyme, there should be a linear relationship between the enzyme reaction time and the amount of the product formed from that reaction. This linearity should be preserved for all enzyme reactions lacking inhibitor or having rapid equilibrium binding events outside of the time window measured. However, the addition of inhibitor may result in a nonlinear progress curve (Figure 11) with an initial burst of enzyme activity (v_i) followed by a final, slower steady-state rate (v_s). Although the steady-state MOA model may still apply under some circumstances, additional characterizations are required.

How can time dependent inhibitors be flagged in the steady-state MOA model?
- For kinetic enzyme assays, the progress curve showing product formation over time is nonlinear (Figure 11).
- For endpoint enzyme assays, time dependent inhibitors can display a noncompetitive phenotype regardless of their true binding modality. Otherwise, they can be identified by observing a shift in inhibitor potency with either a change in the enzyme reaction time and/or a change in the enzyme/inhibitor pre-incubation time.
What is the recommended plan for an appropriate characterization?
- More appropriately characterize and model the nonlinear progress curves (product formed vs time) observed. Illustrations of these progress curves and the appropriate models to use are found below in Figure 11. The resulting fit of the data to the nonlinear model should produce the v_i, v_s, and k_obs for all the [substrate] and [inhibitor] tested.
During this evaluation, k_obs values reflecting timepoints (t) outside of the window tested should be avoided. For example, valid k_obs values from a kinetic run starting at 2 min and ending at 60 min should range between 0.5 min^-1 to 0.08 min^-1. As a general rule, the total time of the reaction should be 5 times greater than 1/k_obs. As a result, the scientist may need to choose a smaller range of [substrate] spanning K_m and [inhibitor] spanning _appK_i.
In most cases, the initial (v_i) and steady-state (v_s) velocities can be fit separately to the steady-state MOA model (presented in the previous section) to yield the binding potency (K_iand/or K_i’ value) and modality for each phase of inhibition.
A more traditional approach to determine the apparent potency of the inhibitor requires the scientist to plot the k_obs values as a function of the [inhibitor] at a fixed [substrate]. This can yield 2 main types of plots illustrated in Figure 12 below: 1) If there is a linear relationship between the k_obs and the [inhibitor] tested, the one-step model shown should be used to determine the _appK_i (potency at the steady-state velocity, v_s). 2) If there is a hyperbolic relationship between the k_obs and the [inhibitor] tested, the two-step model shown should be used to determine the _appK_i (potency at the initial velocity, v_i) and the _appK_i^* (potency at the steady-state velocity, v_s).
A more traditional approach to determine the binding modality of a time dependent inhibitor requires a determination of the _appK_i, from the previous k_obs vs [inhibitor] plot, at each [substrate] spanning the K_m. The _appK_i (and _appK_i*) can then be graphed as a function of [substrate] and fit to the model shown below (Figure 13). The ratio of K_i’/K_i (termed alpha, α) determined from the model below will reflect the binding modality. Inhibitors with alpha values statistically equal to 1.0 are noncompetitive, values statistically less than 1.0 are uncompetitive, and values statistically greater than 1.0 are competitive.

Model to Determine Time Dependent MOA

Image enzymemoa-Image009.jpg

Where possible, we recommend avoiding the iterative fitting into the one-step or two-step models and the model directly above. The scientist should consult with a statistician and enzymologist to perform a global fit of the data to an equation where the one-step or two-step models are solved for the _appK_i shown directly above.

A parallel approach to determine the binding modality requires the scientist evaluate the k_obs values as a function of the [substrate] at a fixed [inhibitor]. The k_obs of a competitive inhibitor will decrease with increasing [substrate] relative to K_m. The k_obs of an uncompetitive inhibitor will increase with increasing [substrate] relative to K_m. The k_obs of a noncompetitive inhibitor will not change with increasing [substrate] relative to K_m). These trends are illustrated in Figure 14.
These methodologies are described in more detail in Chapter 10 of Enzymes 2^nded by Copeland (1). Also be aware that a compound can display both time dependent and tight binding properties. This would require a combination of experiments described above that may require the assistance of a statistician or an experienced enzymologist.

Covalent Modification

During the initial phase of the reaction (initial velocity), there is no buildup of any intermediate other than the enzyme-substrate complex. This assumption most often fails when a compound is an irreversible inhibitor of the enzyme. This type of inhibition can be the result of an immeasurably slow k_off value and/or covalent modification of the enzyme.

How can irreversible inhibitors be flagged in the steady-state MOA model?
- Regardless of their true binding modality, they display a noncompetitive phenotype.
- Irreversible inhibitors are time dependent with v_s values that approach zero. In contrast, reversible time dependent inhibitors have finite, non-zero v_s values. The quality of this observation can be limited by the timepoints measured and the [inhibitor] evaluated.
- The observed k_off value is zero. This can be observed in a plot of the kobs as a function of the [inhibitor], shown in Figure 12. Irreversible inhibitors will yield a y‑int (k_off) of zero.
What is the recommended plan for an appropriate characterization?
- In addition to the characterizations described in the sections above, the scientist can measure the release of inhibitor from the enzyme-inhibitor complex. This is often performed by pre-incubating the enzyme with inhibitor at 10×K_i to achieve 100% inhibition (all enzyme is in the EI complex reflecting v_s), then diluting the assay 30 fold with substrate, and continuously (kinetically) measuring product formation. As illustrated in Figure 15, reversible inhibitors will regain enzyme activity while irreversible inhibitors remain inactive. This experiment can be properly interpreted when 3 controls are included containing 1) no inhibitor throughout to reflect full enzyme activity at the amount of DMSO tested, 2) 10×K_i throughout to achieve 100% inhibition, and 3) 0.3×K_i throughout to reflect the expected amount of inhibition remaining after substrate dilution. Assuming the 10×K_i control is inactive, the final rate (v_s) for the experiment can be divided by the final rate of the 0.3×K_i control to yield the fraction of recovered activity.

It is important to remember the there is no clear distinction between reversible and irreversible time dependent inhibition. The quality of the determination can often reflect the range and density of timepoints measured, [inhibitor] chosen, and other limitations specific to the assay. Therefore, it would be wise for the scientist to consult an analytical chemist to perform a MS-based strategy to confirm irreversible inhibition resulting from covalent modification of the enzyme.

Nonspecific Inhibition

Some compounds may form large colloid-like aggregates that inhibit activity by sequestering the enzyme. These types of compounds can display enzyme dependency, time-dependent inhibition, poor selectivity against unrelated enzymes, and binding modalities that are not competitive. This can be especially problematic when an enzyme is screened against a large diversity of compounds in a screening campaign. Although these compounds do not formally violate the steady-state assumptions, they can generate misleading results which produce inaccurate characterizations of the inhibitor-enzyme complex. The scientist is encouraged to read the Shoichet review published in Drug Discovery Today (3). The chart below was taken from that reference and provides an introduction to the considerations that should be made for evaluating these types of inhibitors.

Image enzymemoa-Image010.jpg

References

Literature Cited

1.: Copeland RA. Enzymes: A Practical Introduction to Structure, Mechanism, and Data Analysis, second edition. 2000, Wiley, New York.
2.: Segal IH. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems. 1975, Wiley, New York.
3.: Shoichet BK. Screening in a Spirit Haunted World. Drug Discovery Today 2006, v11, pgs 607-615. [PMC free article: PMC1524586] [PubMed: 16793529]

Additional References

Copeland RA. Mechanistic Considerations in High-Throughput Screening. Analytical Biochemistry 2003, v320, pgs 1-12. [PubMed: 12895464]
Copeland RA. Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists. 2005, Wiley, New York, [PubMed: 16350889]
Copeland RA, Pompliano DL, Meek TD. Drug-Target Residence Time and Its Implications for Lead Optimization. Nature Reviews Drug Discovery 2006, v5, pgs 730-739. [PubMed: 16888652]
Fehrst A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. 1999, W.H. Freeman, New York.
Kenakin TP. A Pharmacology Primer: Theory, Application, and Methods. 2004, Elsevier, San Diego.
Robertson JG. Mechanistic Basis of Enzyme-Targeted Drugs. Biochemistry 2006, v44, pgs 5561-5571. [PubMed: 15823014]
Swinney DC. Biochemical Mechanisms of Drug Action: What Does It Take For Success? Nature Reviews Drug Discovery 2004, v3, pgs 801-808. [PubMed: 15340390]
Swinney DC. Biochemical Mechanisms of New Molecular Entities (NMEs) Approved by United States FDA During 2001-2004: Mechanisms Leading to Optimal Efficacy and Safety. Current Topics in Medicinal Chemistry 2006, v6, pgs 461-478. [PubMed: 16719803]

Glossary of MOA Terms

The definitions for these terms were gathered from references

Active site: the specific and precise location on the target responsible for substrate binding and catalysis.
Allosteric activators: an allosteric effector that operates to enhance active site substrate affinity and/or catalysis. (Copeland, Enzymes, pg368)
Allosteric effector: small molecule that can bind to sites other than the enzyme active site and, as a result of binding, induce a conformational change in the enzyme that regulates the affinity and/or catalysis of the active site for its substrate (or other ligands). (Copeland, Enzymes, pg368)
Allosteric repressors: an allosteric effector that operates to diminish active site substrate affinity and/or catalysis. (Copeland, Enzymes, pg368)
Allosteric site: a site on the target, distinct from the active site, where binding events produce an effect on activity through a protein conformational change. (Kenakin, A Pharmacology Primer, p195).
Alpha: typically noted as the ratio, K_I’/K_I. It reflects the effect of an inhibitor on the affinity of the enzyme for its substrate, and likewise the effect of the substrate on the affinity of the enzyme for the inhibitor. (Copeland, Enzyme, pg268)
Biochemical assay: the in vitro based mechanism used to measure the activity of a biological macromolecule (enzyme).
Cofactor: nonprotein chemical groups required for an enzyme reaction.
Enzyme: protein that acts as a catalyst for specific biochemical reaction, converting specific substrates into chemically distinct products.
Multivariate fitting: Fitting a more than 2 variable model (Example: Response, [Inhibitor], [Substrate]) to all of the data from a MoA experiment using nonlinear regression.
Inhibitor: any compound that reduces the velocity of an enzyme-catalyzed reaction measured in a biochemical assay, as represented by percent inhibition or IC₅₀.
Initial velocity: the initial linear portion of the enzyme reaction when less than 10% of the substrate has been depleted or 10% of the product has formed. (QB Manual, Section IV, pg5)
In vitro: (to be defined later)
Ligand: a molecule that binds to the target. (Kenakin, A Pharmacology Primer, pg 198)
Linearity: A relationship between two variables that is best described by a straight line. In MoA experiments, the amount of product formed should be linear with respect to time.
Substrate: a molecule that binds to the active site of an enzyme target and is chemically modified by the enzyme target to produce a new chemical molecule (product).
Target: a macromolecule or macromolecular complex in a biochemical pathway that is responsible for the disease pathology. (QB manual, Section XII, pg3)
k_cat: turnover number representing the maximum number of substrate molecules converted to products per active site per unit time. (Fehrst, Str Mech Prot Sci, pg109)
K_I: the affinity of the inhibitor for free enzyme.
K_I’: the affinity of the inhibitor for the enzyme-substrate complex.
K_M: the concentration of substrate at ½ Vmax, according to the Henri-Michaelis-Menten kinetic model (QB manual, Section IV, pg9)
k_off: the off-rate associated with the release of inhibitor from an enzyme-inhibitor complex.
k_on: the on-rate associated with the formation of an enzyme-inhibitor complex.

Footnotes

^*: Edited by James McGee and Jeffrey Weidner

Figures

Figure 1

– Illustrations of data demonstrating Competitive, Noncompetitive, and Uncompetitive Inhibition. The circles represent those rates obtained without the addition of inhibitor. The triangles contained 0.5×K_i of inhibitor, the diamonds contained 2.0×K_i of inhibitor, and the squares contained 4.0×K_i of inhibitor. The black circles depict the shifts in the apparent K_m for each binding modality.

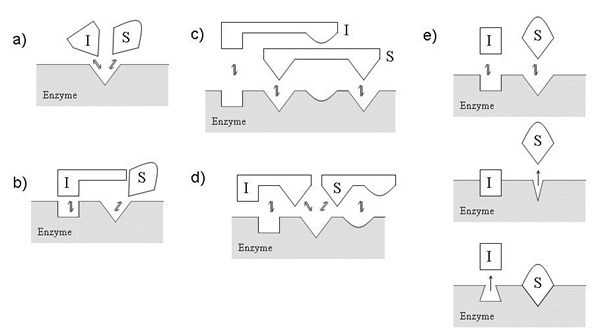
Figure 2

– Examples of Competitive Inhibition where Substrate (S) and Inhibitor (I) binding events are mutually exclusive. (a) Classical model for competitive inhibition where S and I compete for the same precise region of the active site. (b) I does not bind to the active site, but sterically hinders S binding. (c) S and I binding sites are overlapping. (d) S and I share a common binding pocket on the enzyme. (e) I binding can result in a conformational change that prevents S binding (and vice versa). This was adapted from Segal, Enzyme Kinetics.

Figure 3

– Examples of Noncompetitive Inhibition where Inhibitor (I) binding occurs at a site distinct from the Substrate (S) binding site and the Catalytic center (c) of the active site. (a) In this model, the binding of S induces a conformational change to align the catalytic center near S for catalysis. However, when I binds at a separate site, the conformational change does not occur and enzyme activity is inhibited. (b) In this model, I can sterically hinder S binding and release. However, unlike Figure 1-B, I and S can occupy the enzyme at the same time. This was adapted from Segal, Enzyme Kinetics.

Figure 4

– An example of Uncompetitive Inhibition where Inhibitor (I) only binds in the presence of Substrate (S).

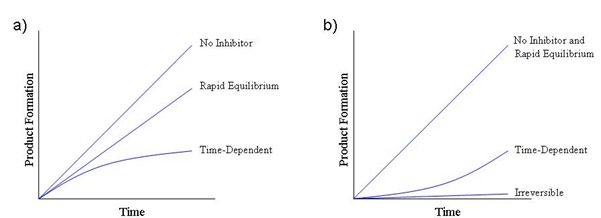
Figure 5

– Illustrations of time-dependent inhibition. (a) This graph depicts the decrease in the initial velocity (product formed vs time) observed for classical, rapid equilibrium inhibitor and a time-dependent inhibitor. The latter yields a nonlinear progress curve consistent with a slow kon value. (b) This graph depicts the recovery of enzyme activity (product formed vs time) following dilution of the enzyme-inhibitor complex with substrate. Dilutions of classical, rapid equilibrium inhibitor complexes recover full activity immediately after dilution. Dilutions of time-dependent inhibitor complexes recover enzyme activity more slowly, indicative of a compound with a slow koff value. Dilutions of irreversible inhibitor complexes maintain the enzyme-inhibitor complex after dilution.

Figure 6

– Classical Steady-State analysis of the mechanism of action. The inhibitor and substrates are serially diluted to achieve concentrations in the assay that span their respective binding constants (K_i and K_m). The addition of enzyme and cofactors will initiate the enzymatic reaction. The order of addition typically depends on the assay in question and may be altered for time-dependent inhibitors (discussed later). The assay incubates for some period of time, the signal is read, the data is fit, and the results are analyzed.

Figure 7

– Residual plots demonstrating the difference in observed rate of enzyme activity (z‑axis) at each concentration of substrate (y-axis) and inhibitor (x-axis) for 2 binding modalities. (a) Competitive Inhibition vs Noncompetitive inhibition. (b) Competitive inhibition vs Uncompetitive inhibition. (c) Noncompetitive vs Uncompetitive inhibition. Taken together, competitive inhibitors are best distinguished from noncompetitive and uncompetitive inhibitors at both high [substrate] and high [inhibitor]. Noncompetitive and uncompetitive inhibitors are best distinguished from each other at [substrate] and [inhibitor] near their binding constants (K_m and K_i). Therefore, the range and density of concentrations tested are both important.

Figure 8

– Comparison on enzyme data for a system with a proper slope of 1 and another displaying a sigmoidal relationship (ex. slope of 2) between the substrate concentration tested and the rate observed.

Figure 9

– Plotting the IC₅₀ vs [Enzyme] will reveal whether a compound is tight binding. As depicted on the left, no change in the IC₅₀ suggests that the compound is not tight binding and the assumption ([I] >> [E]) holds true. As depicted on the right, a change in the IC₅₀ (with a slope of 0.5) suggests that the compound is tight binding and requires additional characterization.

Figure 10

– A plot of the IC₅₀ vs [substrate] will reveal the binding modality for a tight binding inhibitor. The quality of this assessment is predicated on the choice of a range of substrate concentrations that span the K_m. The graph illustrates that competitive inhibition is best identified at substrate concentrations above K_m. In contrast, uncompetitive inhibition is best identified at substrate concentrations below K_m. The true K_i and/or K_i’ values can be obtained from a fit using the model below.

Figure 11

– Progress curves for linear, rapid equilibrium inhibition (left) and nonlinear, time dependent inhibition (right). Nonlinear progress curves resulting from time dependent inhibition can be fit to the model shown above. The resulting fit will yield the initial velocity (v_i), steady-state velocity (v_s), and the rate constant for the interconversion between v_i and v_s (k_obs), under the conditions tested. These values can be used to assess the true binding potency and modality.

Figure 12

– A plot of the k_obs vs [inhibitor] will allow for the determination of the _appK_i value for a time dependent inhibitor. If the relationship between k_obs and the [inhibitor] is linear, the one-step model shown above should be used. If the relationship is nonlinear, the two-step model should be used.

Figure 13

– A plot of the _appK_i (and _appK_i*) vs [substrate] will allow for the determination of the true binding potency and modality. The modeled lines above are generated using the equation shown directly below where alpha = K_i’/K_i.

Figure 14

– A plot of the k_obs vs [substrate] will reveal the binding modality for a time dependent inhibitor. It is important to choose [substrate] well above and below the K_m to improve the ability to best distinguish the true binding modality.

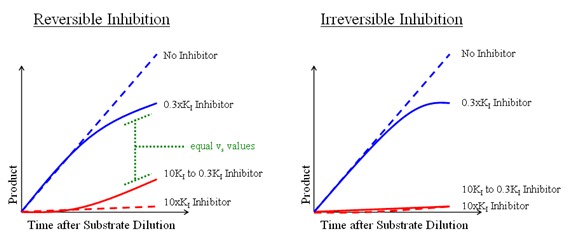
Figure 15

– The recovery of enzyme activity following dilution of the EI complex can be an indication of the reversibility of the inhibitor. Irreversible inhibitors (right) will not recover any enzyme activity following dilution of the EI complex with substrate. In contrast, a reversible inhibitor (left) will recover enzyme activity equivalent to the 0.3×K_i control.

Tables

Table 1:

Summary of competitive, non-competitive and uncompetitive inhibition models.

Inhibition	Description	K_i	K_i’	K_i’/K_i
Competitive	The inhibitor binds only to free enzyme. This binding most often occurs in the active site at the precise location where substrate or cofactor (being evaluated in the MOA study) also binds.	finite	Infinite	infinite
Mixed	These inhibitors display properties of both competitive and noncompetitive inhibition.	finite	Finite	> 1
Noncompetitive	The inhibitor binds equally well to both free enzyme and the enzyme-substrate complex. Consequently, these binding events occur outside the active site.	finite	Finite	= 1
Uncompetitive	The inhibitor binds only to the enzyme-substrate complex at a location outside the active site.	infinite	Finite	= 0

All Assay Guidance Manual content, except where otherwise noted, is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported license (CC BY-NC-SA 3.0), which permits copying, distribution, transmission, and adaptation of the work, provided the original work is properly cited and not used for commercial purposes. Any altered, transformed, or adapted form of the work may only be distributed under the same or similar license to this one.

Bookshelf ID: NBK92001PMID: 22553872

Contents

< Prev Next >

Mechanism of Action Assays for Enzymes*

Authors

Affiliations

Abstract

Overview of MOA in Drug Discovery

Types of Inhibition

Competitive Inhibition

Noncompetitive Inhibition

Uncompetitive Inhibition

Allosteric Inhibition

Partial Inhibition

Tight-Binding Inhibition

Time-Dependent Inhibition

Performing MOA Studies

Classical Steady-State Experiments

Guidelines for Assay Design

Statistical Validation of the Designed Assay

Guidelines for Running the Assay

Guidelines for Data Fitting and Interpretation

When the Steady-State Assumptions Fail

Tight Binding Inhibition

Time-Dependent Inhibition

Covalent Modification

Nonspecific Inhibition

References

Literature Cited

Additional References

Glossary of MOA Terms

Footnotes

Figures

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

Figure 11

Figure 12

Figure 13

Figure 14

Figure 15

Tables

Table 1:

Mechanism of Action Assays for Enzymes^*